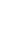Реологические Свойства Бетона

В настоящей статье будут рассмотрены реологические свойства бетона и их формулы расчета. Многие реальные тела не обладают каким-либо одним механическим свойством. Процесс их деформирования (уплотнения) бывает сложен, а деформативные характеристики занимают некоторое промежуточное положение между вязкими жидкостями и Твердыми телами. Такие сложные системы, к которым относится и бетонная смесь, во времени при различных нагрузках (напряженно-деформированном состоянии) ведут себя неоднозначно и характеризуются реологическими свойствами. При описании реологических свойств обычно используют упругость, пластичность и вязкость (модели Гука, Сен-Венана, Ньютона). Основные понятия об этих свойствах рассматриваются в работах по физико-химической механике. Наряду со свойствами коллоидных частиц свойства бетонных смесей определяются их составом, водоцементным отношением, вводимыми в состав бетонных смесей поверхностно-активными веществами (ПАВ). Второй, столь же важный фактор, - напряженно-деформированное состояние, от которого зависит, какие из свойств бетонных смесей будут проявляться.

При изучении реологических свойств бетона, в качестве примера, рассмотрим зависимость между напряжениями и деформациями в затвердевшем бетоне (рис. 1). На участке ОА происходит упругая деформация образца с модулем упругости E_b=σ_A/ε_A, на участке AB Появляется пластическое течение. Если в точке В разгрузить образец, то останется остаточная часть деформации ε_ОСТ характеризующая пластические изменения в бетоне.бетона.

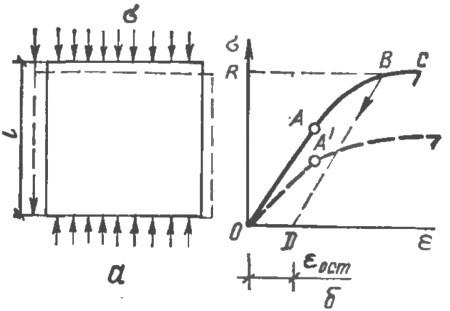
Рис. 1. Испытание на одноосное сжатие бетонного образца: α - схема испытания; б - зависимость напряжение-деформация»

На участке ВС протекает только пластическая деформация. В зависимости от длительности процесса диаграмма трансформируется: при длительном приложений нагрузки значительно уменьшается уровень, характеризующий предел текучести σТ (прочность материала R). В этом случае на диаграмме «σ-ε» будут преобладать пластические деформации, их значения значительно увеличатся, увеличатся и остаточные деформации εОСТ, может измениться также модуль упругости (участок ОА). Аналогичные изменения произойдут при сжатии бетонной смеси в замкнутом сосуде.

В зависимости от вида напряженно-деформированного состояния могут быть использованы различные модели состояния (Гука, Ньютона, Кулона, Сен-Венана). Так, для случая подвижных виброорганов, так называемых вибронасадков, при описании процесса формирования, которое определяется истечением через вибрационную щель, используется модель Ньютона, в более сложных напряженных состояниях - модель Бингама или Кельвина - Фойгта.

Характер зависимости между нормальными и касательными (сдвиговыми) напряжениями (рис. 2) записан Кулоном в следующем виде:

τ=τ₀+σtgφ,

где τ₀ - предельное напряжение сдвига; σ - нормальные напряжения; φ - угол внутреннего трения.

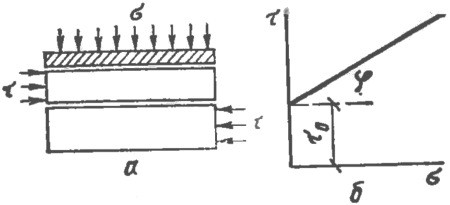
Рис. 2. Испытание на сдвиг бетонного образца: α - схема испытания; б - зависимость между нормальными и касательными (сдвиговыми) напряжениями

При определении удобоукладываемости целесообразно оценить значение предельного напряжения сдвига то, которое в зависимости от осадки конуса или жесткости бетонных смесей может Изменяться в пределах от 50 до 1500 Па. По данным Л. А. Файтельсона для бетонов с осадкой конуса 1...7 см предельное напряжение сдвига составляет от 2000 до 14 000 Па. Эти предельные характеристики τ₀ сравнили с численными значениями вязкости, получаемыми при других методах измерения. Предельное напряжение сдвига или, в самом общем виде, предел текучести зависит от степени коагуляции или кристаллизации цементного теста, а также от зацепления (сцепления) мелкого и крупного заполнителя между собой.

Модель Кулона бывает целесообразна для описания поведения не только бетонной смеси, НО и отформованного бетона при немедленной распалубке Изделий. Тогда значение τ₀ и угол внутреннего трения φ определяют возможную высоту формирования изделий из жестких или вакуумированных бетонных смесей.

Одно из важных свойств бетонной смеси - вязкость, характеризующаяся сопротивлением деформации сдвига или скольжения одного слоя по другому. Это может быть также и сопротивление при данной оптимальной скорости деформации от действия нормальных напряжений. Модель Ньютона выражается уравнением состояния

σ=vε,

где v - коэффициент вязкости; ε - скорость относительной деформации.

Для случая вязких жидкостей зависимость между σ и ε носит линейный характер, величина v (или v_Н) характеризует коэффициент вязкости (рис. 3). В более общем случае в структурированных дисперсных системах возникает структурная вязкость v_СТР. Ее можно преодолеть в процессе вибрационного уплотнения только при определенном значении ε. Тогда вязкость в точке Е согласно зависимости Ньютона будет выражена осредненным значением коэффициента вязкости псевдожидкости v_П.

Рис. 3. Испытание на вязкость бетонного образца: α - модель Ньютона; б - зависимость «напряжение - скорость деформации»; 1 - вязкая жидкость; 2 - псевдожидкость

Величины τ₀ (σ_m) и v_СТР характеризуют сопротивление деформированию в структурированных дисперсных системах. Их природа определяется силами сцепления коагулированных систем, в которых развиваются процессы кристаллизации. В ряде случаев эти две разные характеристики совместно участвуют в процессе сопротивления при формировании бетонных смесей, поэтому сложно выделить влияние σ_m или v_СТР на общий процесс формообразования или уплотнения.

Модель Бингама представляет собой последовательное соединение упругого, пластического и вязких элементов. Уравнение состояния такого тела можно представить в следующем виде:

ε=σ/Е при σ<σm;

ε=(((σ-σ_m)t)/v)+σ/Е приσ>σ_m

(σ_m - предел текучести; v - коэффициент вязкости системы).

Модель среды Бингама во многих случаях удовлетворительно характеризует свойства растворных и бетонных смесей.

Исследования авторов в основном базируются на модели Кельвина - Фойгта, представляющей собой параллельное соединение упругих и вязких элементов. В этом случае сила N необходима для деформирования (уплотнения) бетонной смеси:

N=EFε+H*(дε/дt),

где F - площадь уплотняемого столба; Н - вязкое сопротивление по высоте столба бетонной смеси; дε/дt - скорость деформации.

Складывая силы, действующие на элемент столба бетонной смеси толщиной dx (рис. 4), получим:

N+(дN/дx)-N-mдx(д²u/дt²)=0;

дN/дx=m(д²u/дt²)

(u - перемещения слоя при вибровоздействии).

Используя представления Кельвина - Фойгта о силе N, получим для всего столба с учетом вынуждающей гармонической силы Q cos ωt, действующей в нижней части столба, следующее выражение:

m(д²u/дt²)-H(д³u/дx²дt)+EF(д²u/дx2)=Qcosω₀t

Для определения собственных колебаний при виброуплотнении приведем уравнение к единичному столбу бетонной смеси, разделив на F:

ρ(д²u/дt²)-E(д²u/дx)+q(д³u/дx²дt)=0

где ρ=m/F - удельная погонная масса бетонной смеси; q=H/F - коэффициент вязкого трения в единичном столбе.

Изучение волновых явлений на высоком столбе бетонной смеси представляет самостоятельную задачу теории вибрационного уплотнения. Поскольку в таком высоком столбе реализуются различные волновые процессы (различные перемещения u, ускорения A_g), столб оказывает в разных сечениях различное давление N, определяющее в конечном счете степень уплотнения и прочностные свойства бетона.

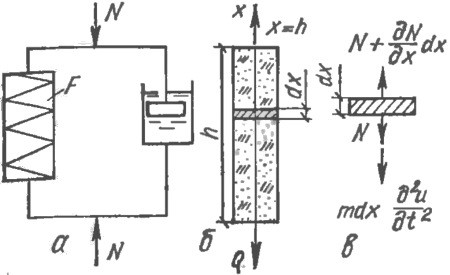
Рис. 4. Уплотнение столба бетонной смеси: α - модель Кельвина - Фойгта; б - схема столба бетонной смеси; в - схема действия сил при виброуплотнении