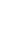Каменные арки и своды, являвшиеся в прошлом основными видами перекрытия проемов в стенах и помещений в зданиях, в настоящее время почти полностью вытеснены железобетонными, железо-кирпичными или стальными балочными конструкциями. Они сохранились в новом строительстве только в виде плоских сводиков между стальными балками или для перекрытия небольших пролетов между несущими стенами. В отдельных случаях эти старинные конструкции вводятся в современные проекты из архитектурных соображений.
По своей статической схеме каменные арки и своды относятся в отношении расчета в наиболее сложным конструкциям. Детальное изучение расчета этих конструкции затрудняется кроме того большим разнообразием разновидностей этих конструкций, созданных нашими предшественниками для разрешения сложных задач, которые сейчас конструктор обычно решает в металле или железобетоне. Мы рассмотрим решения только основных видов арок и сводов.
Точный расчет арок и сводов, не имеющих в местах опирания шарниров, возможен только по методам строительной механики с учетом упругих деформаций материала. Недостатком этих точных расчетов является их большая сложность. К тому же точности метода не соответствует степень достоверности основных предпосылок расчета. Модуль упругости является переменной величиной, зависящей не только от величины напряжений, но и от направления усилий относительно плоскости швов кладки. Последние же в силу особенностей разрезки кладки арок и сводов имеют для отдельных частей конструкций различное направление; в результате мы не получаем однородного упругого тела.
Поэтому целесообразно пользоваться более простыми методами расчета, которые должны в то же время обеспечить достаточную надежность сооружения.
Конструирование арок и сводов в прошлом достигло высокой ступени развития еще до создания современных методов строительной механики, основанных на законах деформации упругого тела. Были найдены приемы приближенного расчета, которые дали возможность возвести замечательные памятники архитектуры с относительно небольшими запасами прочности и с хорошим использованием несущих свойств кладки. Эти методы преимущественно были графическими. На основе анализа их и использования современной строительной механики могут быть созданы современные приближенные методы расчета арок и сводов, дающие простое, но достаточно надежное решение. Для более ответственных случаев, например для расчета арочных каменных мостов, арок и сводов больших пролетов с большими нагрузками и т. п., требуется точное решение методами строительной механики.
При конструировании арок и сводов прежде всего вызывает затруднение назначение предварительных размеров, по которым должен производиться расчет. Для этой цели могут быть использованы опыт прошлого строительства и эмпирические формулы, отображающие уже возведенные и оправдавшие себя долголетней работой сооружения.
Не входя в детальную классификацию сводов, которая составляет предмет курса архитектуры, мы отметим только некоторые основные подразделения, имеющие значение для расчета и конструирования. Решающее значение для величины распора и статической работы арки и свода имеет высота подъема.
По отношению высоты подъема f к пролету l различают следующие виды арок и сводов:
- возвышенные и стрельчатые (рис. 1, а) при f > ½ l; 1;
- полуциркульные (рис. 1, б) при f = ½ l;
- пологие (рис. 1, в) при f, в пределах от ½ l до ⅙ l (в среднем f = ⅓ l);
- плоские (рис. 1, г) при f в пределах от ⅙ l до 1/12 l (в среднем f =⅛ l).
Выбор вида свода или арки определяется главным образом архитектурными соображениями; однако необходимо учитывать и работу свода как конструкции.
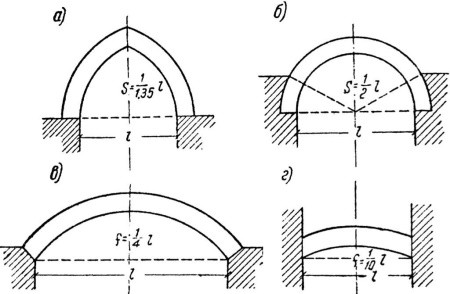
Рис. 1. Основные виды арок: а - стрельчатая; б - полуциркульная; в - пологая; г - плоская
Чем меньше отношение подъема к пролету, тем больше распор. Большой распор делает более постоянным положение линии давления в своде при изменениях положения нагрузки и приближает ее в средней линии. При этом возникают трудности в погашении распора. Из-за большого распора очень плоские своды f = (1/10 l) - (1/12 l) применяются только при малых пролетах (до 3 м). При пролете более 3 м выбирают подъем свода f = ⅙ l - ⅛ l. При больших пролетах и нагрузках (l > 6 м) предпочтительнее пологие своды с подъемом f = ⅓ l - ⅕ l.
Очертание свода принимается по дуге круга по параболе, эллипсу и по сложным кривым, представляющим собой сочетание отрезков дуг круга (коробовые кривые). Толщина свода от замка в пяте увеличивается плавно или уступами. Чаще всего предпочитают пользоваться дугами круга, удобными для разбивки при производстве работ. Для верхней и нижней кривых принимают дуги кругов, описанных из различных центров для получения утолщения свода пятам. При расчете ось свода принимается по средней кривой, которая приближается в параболе.
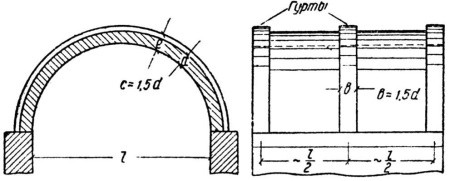
Рис. 2. Усиление тонких сводов гуртами, повышающими их устойчивость и прочность
Для повышения устойчивости тонких сводов при большом отношении пролета к толщине, чтобы не утолщать всего свода, делаются гурты или утолщенные криволинейные поперечные пояса, выступающие над верхней поверхностью свода (рис. 2). Расстояние между гуртами обычно назначают равным половине пролета свода. Ширина и толщина гурта (считая толщину вместе с толщиной свода) делаются примерно равной полуторной толщине свода.
Для сводов малых пролетов с нагрузкой сверх веса свода до 500 кг/м2 (забутка, пол и полезная нагрузка) толщина свода ориентировочно может быть назначена по таблице на рис. 3 с последующей проверкой расчетом.
Для ненагруженных сводов верхних покрытий толщины могут быть уменьшены, для сильно нагруженных должны быть увеличены. Толщина арок принимается ориентировочно в 1,5 раза больше толщины сводов, указанных на рис. 3.

Рис. 3. Ориентировочные толщины сводов для междуэтажных перекрытий (в кирпичах)